Contenidos:
Estudio de las ecuaciones de 2 grado y cómo usar la aplicación
Posibles casos de Ecuaciones de Segundo Grado
Casos de Ecuaciones Incompletas
Casos definidos por el Discriminante
Fracciones en la aplicación Ecuacion2G
Calculadora de Ecuaciones de 2º Grado:
Aplicación que resuelve todas las ecuaciones de segundo grado.
Calculadora de Ecuaciones de 2º Grado | Ecuacion2G : Aplicación que resuelve todas las ecuaciones de segundo grado.
Si te descargas la aplicación también te descargas este artículo en fomato pdf.
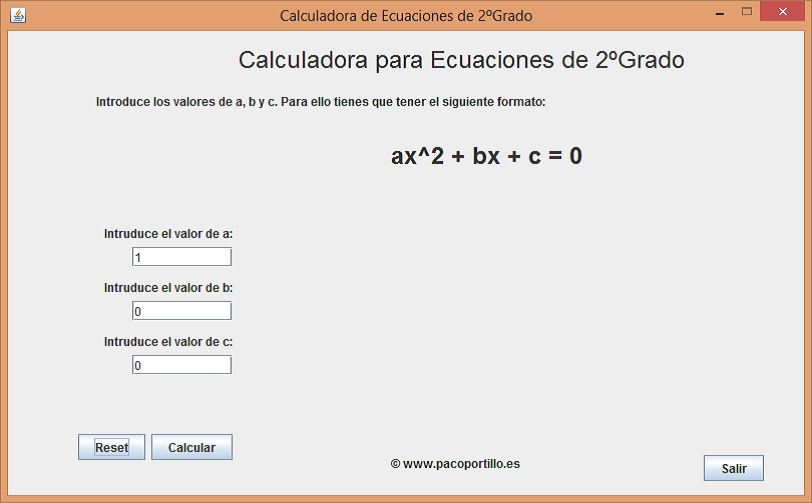
Estudio de las ecuaciones de 2 grado y cómo usar la aplicación:
Una ecuación de segundo grado es toda expresión de la forma:
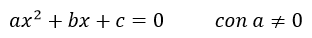
Escrito de otra forma equivalente sería:
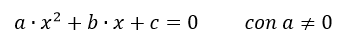
Donde tendremos que averiguar la incógnita ‘x’ y los datos que debemos introducir son a, b y c.
Donde ‘a’ no puede ser cero porque anularía la ‘x^2’ o sea la x al cuadrado.
La solución viene dada por dos posibles soluciones a ‘x’.
Veamos un primer ejemplo:
Por ejemplo si resolvemos en la aplicación Ecuacion2G, la siguiente ecuación:
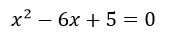
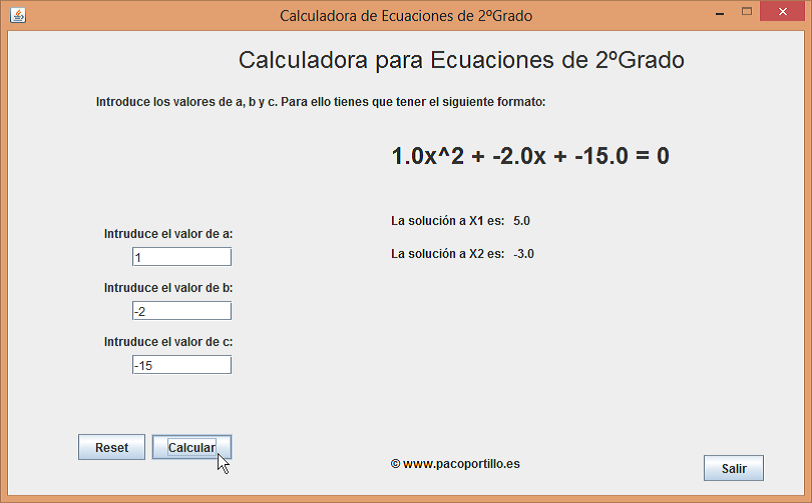
Tendremos que introducir los parámetros para a=1, b=-6 y c=5. De la siguiente manera:
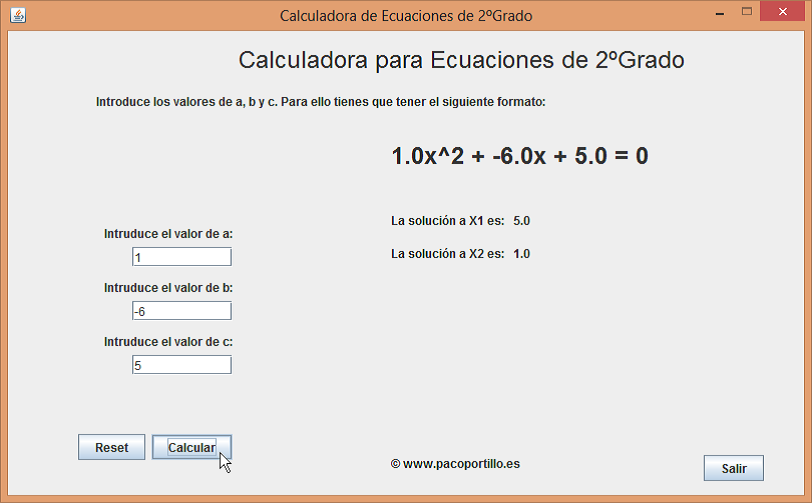
Pero si lo queremos resolver del modo tradicional debemos emplear la siguiente fórmula:
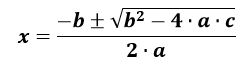
Y se haría de la siguiente manera:
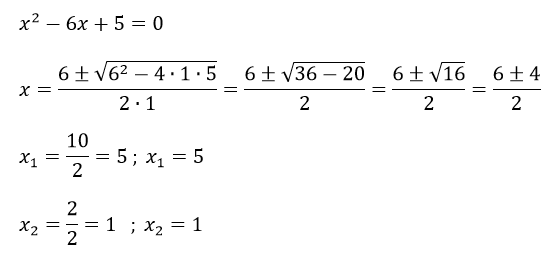
Y la comprobación de las soluciones de ‘x’ sería:
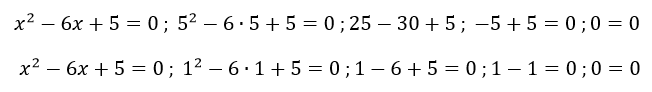
Formatear la ecuación:
Puede que la ecuación no nos llegue en el formato arriba indicado. En ese caso debemos despejar o hacer lo necesario para llegar a la expresión indicada. Por ejemplo:
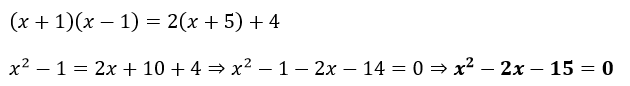
A partir de aquí ya podemos resolver:
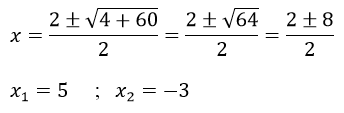
Posibles casos de Ecuaciones de Segundo Grado:
Sí ‘a es menor que 0’:
Ver
Sí ‘a es menor que 0’ tenemos que multiplicar los dos miembros de la igualdad por (-1)
Por ejemplo:
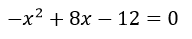
Y se resolvería así:
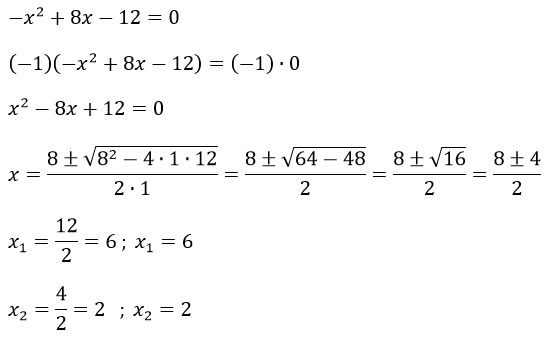
Los valores a introducir en la aplicación Ecuacion2G serían los valores -1, 8 y -12:
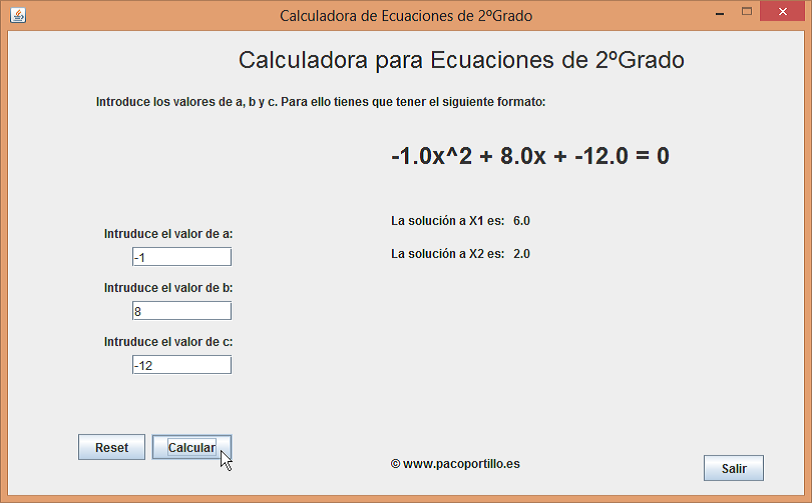
Casos de Ecuaciones Incompletas:
Ver
Otros casos serían la resolución de ecuaciones incompletas: una ecuación de segundo grado es incompleta cuando alguno de los coeficientes: b o c, o ambos, son iguales a cero, por tanto podemos encontrarnos con tres tipos de ecuaciones de segundo grado incompletas.
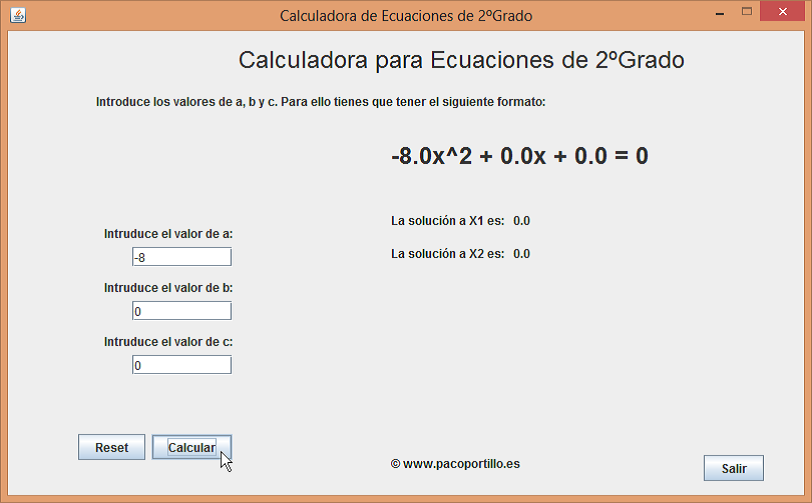
- Si sólo existe ‘a’ (recordamos que ‘a’ es el único coeficiente que debe existir):
En este caso la ecuación sólo tiene una solución y siempre es 0.
Por ejemplo:
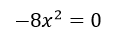
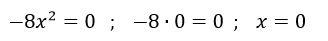
- Si no existe ‘c’:
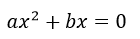
Para resolverlo al modo tradicional extraemos el factor común ‘x’:
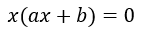
Al tener esta igualdad a cero, un factor es cero seguro y el otro podría serlo también:
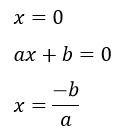
Por ejemplo:
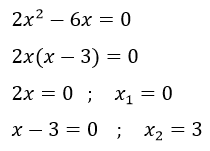
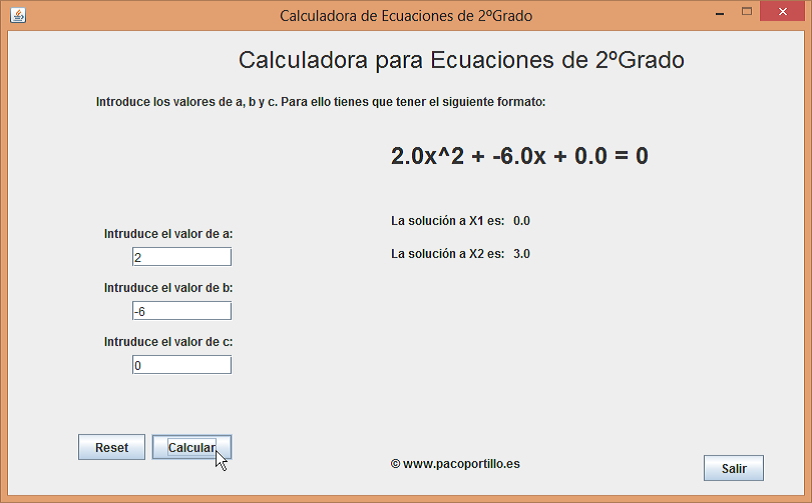
En la aplicación Ecuación2G se reduce a introducir los siguientes parámetros:
- Si no existe ‘b’:
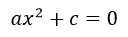
Para resolverla pasamos el término ‘c’ al segundo miembro cambiando su signo:
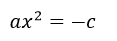
Después pasamos el coeficiente ‘a’ al segundo término y pasa dividiendo.
Despejamos el cuadrado de la ‘x’ pasándole como raíz cuadrada:
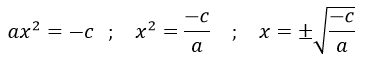
Por ejemplo:
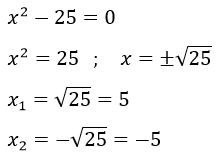
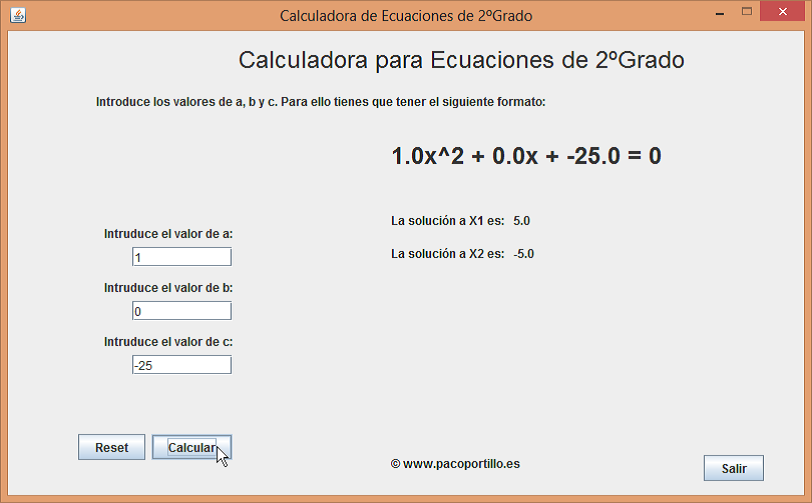
En la aplicación se resolvería de la siguiente manera, mucho más sencillo:
Casos definidos por el Discriminante:
Ver
Los otros posibles casos serían definidos por el Discriminante. Tenemos la fórmula cuadrática que nos sirve para la obtención general de las soluciones:
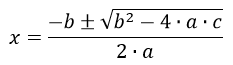
El Discriminante es la expresión contenida dentro de la raíz en la fórmula anterior:
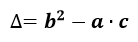
Tenemos tres casos posibles en función del valor del Discriminante:
- Si el Discriminante es mayor que 0:
La ecuación tiene dos soluciones, que son números reales distintos.
Por ejemplo:
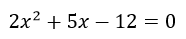
En la aplicación se resolvería:
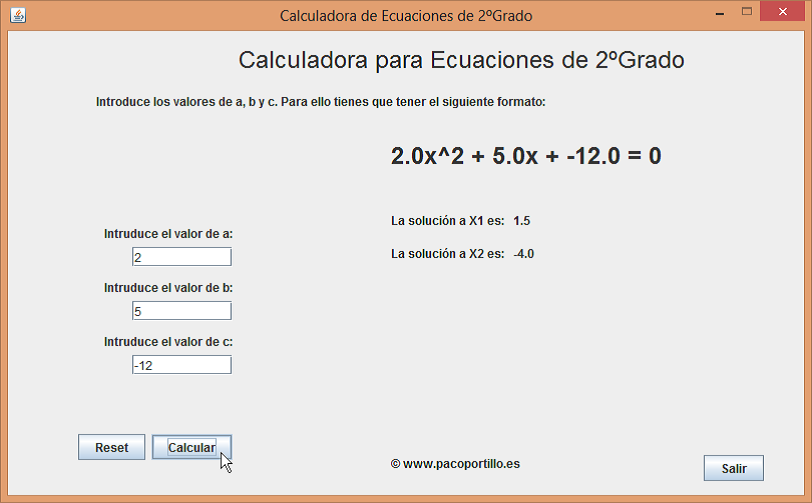
Y de forma tradicional se resuelve del siguiente modo:
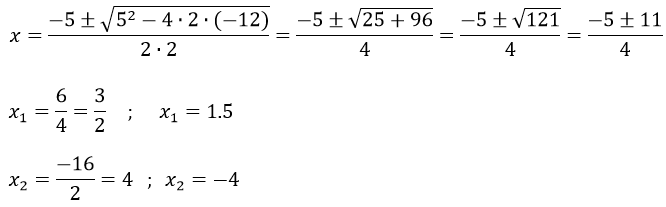
- Si el Discriminante es igual que 0:
La ecuación tiene la misma solución para la las dos ‘x’.
Por ejemplo:
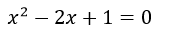
La solución sobre el papel es ésta:
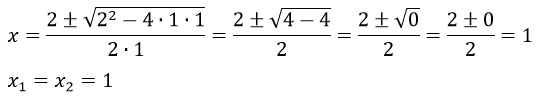
La solución en la aplicación Ecuacion2G sería:
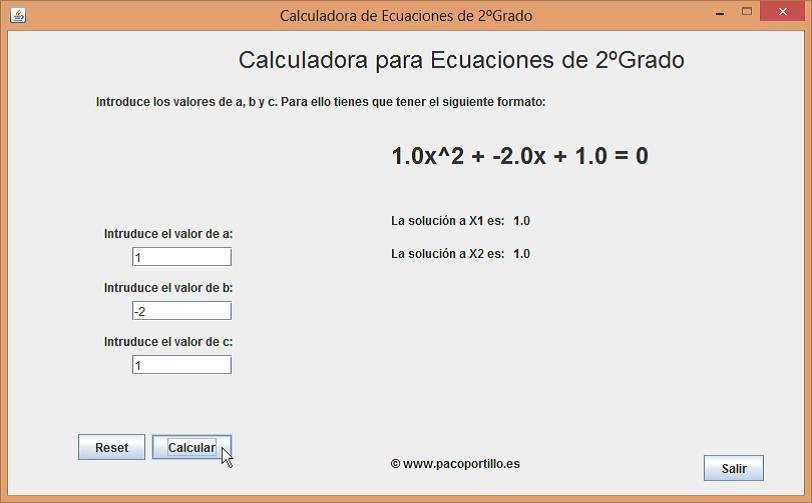
- Si el Discriminante es menor que 0:
La ecuación no tiene soluciones reales. El radicando de una raíz no puede ser un número negativo.
Ejemplo:
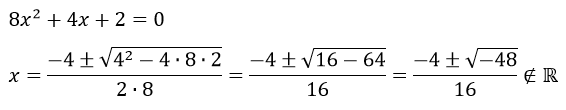
La solución en la aplicación es:
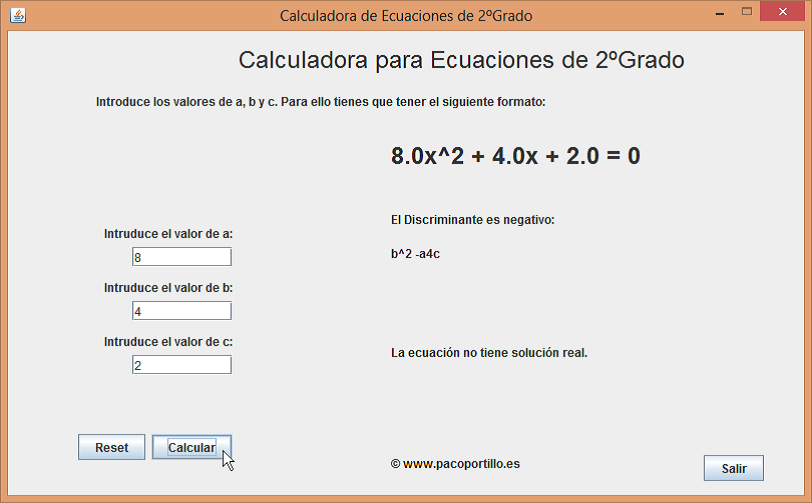
Propiedades de las soluciones:
La suma de las soluciones de una ecuación de segundo grado:
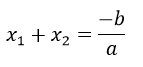
El producto de las soluciones de una ecuación de segundo grado:
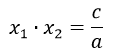
Fracciones en la aplicación Ecuacion2G:
Las fracciones debemos pasarlas a un número decimal.
Por ejemplo:
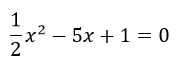
Esto se configuraría en la aplicación con los siguientes parámetros: